数组专题
704.二分查找
题目
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4示例2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1思路
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是
while(left < right)还是while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
题目对于这个问题的决定就主要看题目是什么类型的区间定义了,要始终看区间定义的合理性还有边界值是否有可比较性决定代码写法
我的代码
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right){
int middle = (left + right) / 2;
if(target < nums[middle]) {
right = middle - 1;
}else if(target > nums[middle]) {
left = middle + 1;
}else{
return middle;
}
}
return -1;
}
}官方推荐
javaclass Solution { public int search(int[] nums, int target) { int left = 0, right = nums.length - 1; while (left <= right) { int mid = (right - left) / 2 + left; int num = nums[mid]; if (num == target) { return mid; } else if (num > target) { right = mid - 1; } else { left = mid + 1; } } return -1; } } 作者:力扣官方题解 链接:https://leetcode.cn/problems/binary-search/solutions/980494/er-fen-cha-zhao-by-leetcode-solution-f0xw/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
27.移除元素
题目
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。。
思路
要知道数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
我的代码
javaclass Solution { public int removeElement(int[] nums, int val) { int fastIndex = 0, slowIndex = 0; for(;fastIndex < nums.length && slowIndex < nums.length;fastIndex++) { if(nums[fastIndex] != val){ nums[slowIndex++] = nums[fastIndex]; } } return slowIndex; } }官方推荐
javaclass Solution { public int removeElement(int[] nums, int val) { int n = nums.length; int left = 0; for (int right = 0; right < n; right++) { if (nums[right] != val) { nums[left] = nums[right]; left++; } } return left; } } 作者:力扣官方题解 链接:https://leetcode.cn/problems/remove-element/solutions/730203/yi-chu-yuan-su-by-leetcode-solution-svxi/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
977.有序数组的平方
题目
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
- 输入:nums = [-4,-1,0,3,10]
- 输出:[0,1,9,16,100]
- 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2:
- 输入:nums = [-7,-3,2,3,11]
- 输出:[4,9,9,49,121]
思路
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
==那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间==。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果
A[i] * A[i] < A[j] * A[j]那么result[k--] = A[j] * A[j];。如果
A[i] * A[i] >= A[j] * A[j]那么result[k--] = A[i] * A[i];。我的代码
javaclass Solution { public int[] sortedSquares(int[] nums) { int left = 0 , right = nums.length - 1; int k = nums.length - 1; int[] newNums = new int[nums.length]; while(k >= 0){ if(nums[left] * nums[left] > nums[right] * nums[right]){ newNums[k--] = nums[left] * nums[left]; left++; }else{ newNums[k--] = nums[right] * nums[right]; right--; } } return newNums; } }官方推荐
javaclass Solution { public int[] sortedSquares(int[] nums) { int n = nums.length; int[] ans = new int[n]; for (int i = 0, j = n - 1, pos = n - 1; i <= j;) { if (nums[i] * nums[i] > nums[j] * nums[j]) { ans[pos] = nums[i] * nums[i]; ++i; } else { ans[pos] = nums[j] * nums[j]; --j; } --pos; } return ans; } } 作者:力扣官方题解 链接:https://leetcode.cn/problems/squares-of-a-sorted-array/solutions/447736/you-xu-shu-zu-de-ping-fang-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
###209.长度最小的子数组【中等】
题目
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
- 输入:s = 7, nums = [2,3,1,2,4,3]
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
思路
滑动窗口
接下来就开始介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
==首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。==
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
我的代码
javaclass Solution { public int minSubArrayLen(int target, int[] nums) { int result = Integer.MAX_VALUE; int sum = 0; int left = 0; for(int right = 0; right < nums.length; right++){ // 计算滑动窗口中的总和 sum += nums[right]; // 用while不是if是因为引起窗口总值满足条件的是最后一个元素并不一定是此时窗口的第一个元素,因此只滑动一个单位不能保证 while(sum >= target){ // 在这个while里的每一次循环子序列都达到要求,因此每一次都得更新result result = Math.min(result, right - left + 1); sum -= nums[left++]; } } return result == Integer.MAX_VALUE ? 0 : result; } }官方推荐
javaclass Solution { public int minSubArrayLen(int s, int[] nums) { int n = nums.length; if (n == 0) { return 0; } int ans = Integer.MAX_VALUE; int start = 0, end = 0; int sum = 0; while (end < n) { sum += nums[end]; while (sum >= s) { ans = Math.min(ans, end - start + 1); sum -= nums[start]; start++; } end++; } return ans == Integer.MAX_VALUE ? 0 : ans; } } 作者:力扣官方题解 链接:https://leetcode.cn/problems/minimum-size-subarray-sum/solutions/305704/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
59.螺旋矩阵II【中等】
题目
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:

输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
思路
这道题目可以说在面试中出现频率较高的题目,本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。
大家还记得我们在这篇文章数组:每次遇到二分法,都是一看就会,一写就废 (opens new window)中讲解了二分法,提到如果要写出正确的二分法一定要坚持循环不变量原则。
而求解本题依然是要坚持循环不变量原则。
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
那么我按照左闭右开的原则,来画一圈,大家看一下:
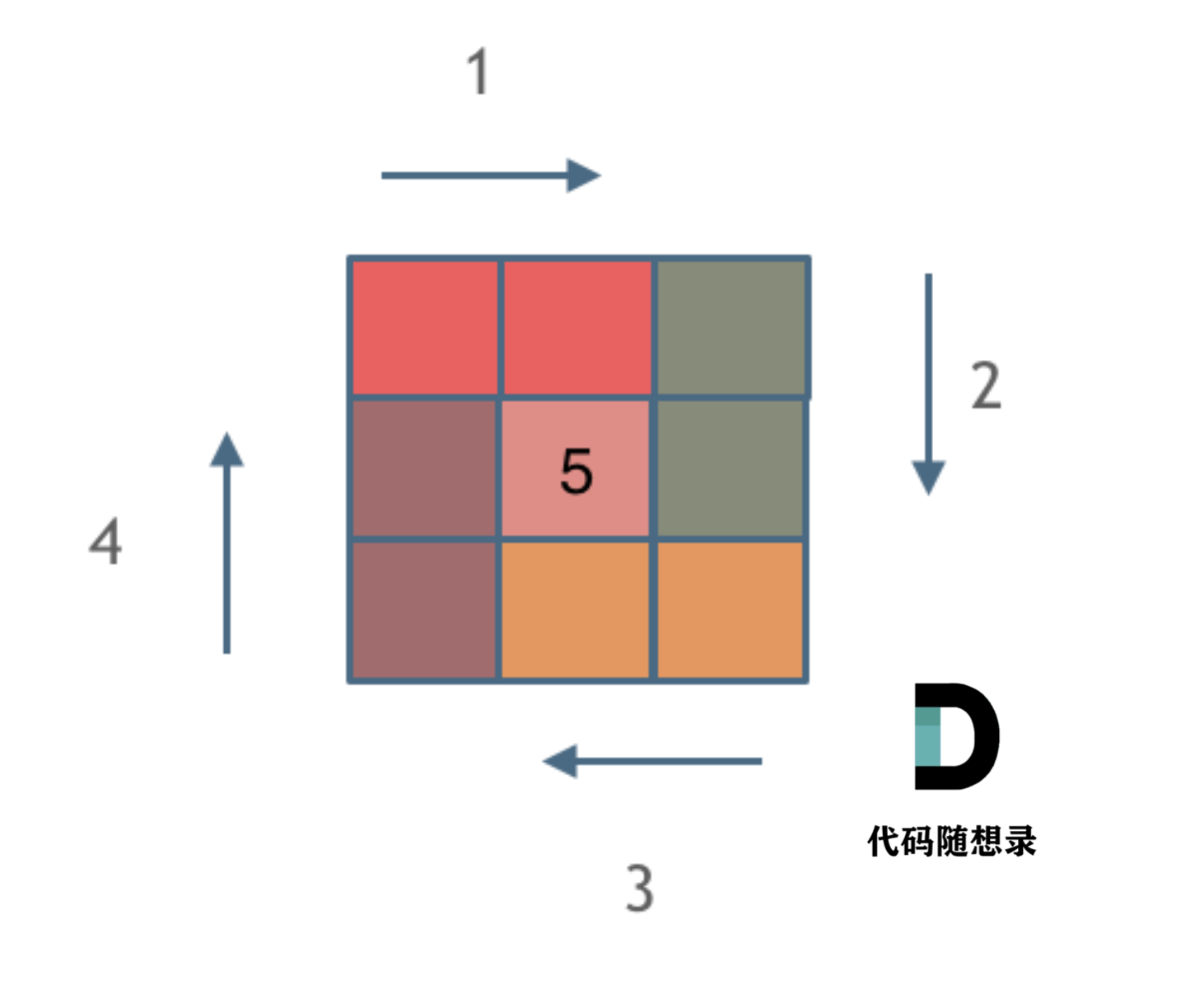
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。==这张图就是理解的重点,他做到了每一条边处理的规则都是一样的==。
我的代码(我把n着重看做边长来对待),
javapublic class Solution { public int[][] generateMatrix(int n) { int loop = n / 2; int radius = n % 2; int i = 0, j = 0; // i行j列 (i,j)就表示当前所在位置 int[][] matrix = new int[n][n]; int count = 1; // 要填充的数字 int startX = 0, startY = 0; // 以左上角为起点 // 按照左闭右开,每一条边的处理规则都是这样,这就是控制循环变量不变 while (loop >= 1) { i = startX; j = startY; // 上边 for (; j < n - 1; j++) { matrix[startX][j] = count++; } // 右边 for (; i < n - 1; i++) { matrix[i][j] = count++; } // 下边 for (; j > startX; j--) { matrix[i][j] = count++; } // 左边 for (; i > startY; i--) { matrix[i][j] = count++; } // 一圈结束,相当于把最外一层空壳正方形扔掉,留下剩余的部分 // 点(startX,startY)按照意义(正方形左上角)因此产生相应变化 loop--; startX++; startY++; // (i,j)在每一圈开始时就是在(startX,startY)处,因此在拆去上一圈外壳的时候,(j,j)已经移动,因此只要再减去1边长就够了 n--; } if (radius == 1) { // 表示边长是奇数,说明最后一个格子需要单独去填 matrix[startX][startY] = count; } return matrix; } }官方推荐
javaclass Solution { public int[][] generateMatrix(int n) { int[][] nums = new int[n][n]; int startX = 0, startY = 0; // 每一圈的起始点 int offset = 1; int count = 1; // 矩阵中需要填写的数字 int loop = 1; // 记录当前的圈数 int i, j; // j 代表列, i 代表行; while (loop <= n / 2) { // 顶部 // 左闭右开,所以判断循环结束时, j 不能等于 n - offset for (j = startY; j < n - offset; j++) { nums[startX][j] = count++; } // 右列 // 左闭右开,所以判断循环结束时, i 不能等于 n - offset for (i = startX; i < n - offset; i++) { nums[i][j] = count++; } // 底部 // 左闭右开,所以判断循环结束时, j != startY for (; j > startY; j--) { nums[i][j] = count++; } // 左列 // 左闭右开,所以判断循环结束时, i != startX for (; i > startX; i--) { nums[i][j] = count++; } startX++; startY++; offset++; loop++; } if (n % 2 == 1) { // n 为奇数时,单独处理矩阵中心的值 nums[startX][startY] = count; } return nums; } }
数组总结
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。因为数组内存空间的地址是连续的。但同时,正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。因此,所谓的删除数组中的元素,其实数组的元素是不能删的,只能覆盖。
对于java,二维数组
int[][] rating = new int[3][4];在内存空间上不是简单的3*4的连续地址空间
所以Java的二维数组在内存中不是
3*4的连续地址空间,而是三条连续的地址空间组成!对于==二分法==,要注意循环不变量原则,只有在循环中坚持对区间的定义,才能清楚的把握循环中的各种细节。二分法是算法面试中的常考题,建议通过这道题目,锻炼自己手撕二分的能力。
对于==双指针法(快慢指针法)==,通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
数组在内存中是连续的地址空间,不能释放单一元素,如果要释放,就是全释放(程序运行结束,回收内存栈空间)。
在数组和链表的操作中是非常常见。
对于==滑动窗口==,主要要理解滑动窗口如何移动 窗口起始位置,达到动态更新窗口大小的,从而得出长度最小的符合条件的长度。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
对于==模拟行为==,不涉及到什么算法,就是单纯的模拟,考察对代码的掌控能力。
总结为: