1-88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 **注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
解法思路及注意点
- 不要总是想着先对特殊情况的处理,很容易想着特殊情况而影响做题速度。尽管确实有一些特殊情况不需要多余的判断逻辑,但是很多时候往往有一套解决方法
- 这道题的关键在于 非递减 排序的元数组最重要合并成 非递减 顺序的结果,因此可以直接 从最大值倒序向前排列
最终代码
public void merge(int[] nums1, int m, int[] nums2, int n){
int p = m - 1, q = n - 1;
int tail = m + n - 1;
int curVal;
while(p >= 0 || q >= 0){
if(p == -1){
// p 遍历结束
curVal = nums2[q--];
}else if(q == -1){
// q 遍历结束
curVal = nums1[p--];
}else if(nums1[p] > nums2[q]){
// 当前nums1比nums2的大
curVal = nums1[p--];
}else{
curVal = nums2[q--];
}
// 插入值
nums1[tail--] = curVal;
}
}2-27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。 假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。 - 返回
k。
解法思路及注意点
双指针,快指针遍历原数组而慢指针只需要在满足当前值不等于目标值时记录,最终慢指针指向的位置就是最终结果的长度
最终代码
public int removeElement(int[] nums, int val) {
// 双指针,快指针指向原来数组,慢指针指向最终结果
// 只需要把不等于val的值放入最终结果
int fast = 0, low = 0;
for(; fast < nums.length && low < nums.length; fast++){
if(nums[fast] != val){
nums[low++] = nums[fast];
}
}
// 最后low指针指向的就是最终结果的长度
return low;
}3-26. 删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你**原地** 删除重复出现的元素,使每个元素 **只出现一次 ** ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
解法思路及注意点
和27类似,双指针即可
最终代码
public int removeDuplicates(int[] nums) {
if(nums.length == 1){
return 1;
}
int pre = nums[0];
int cur;
int low = 1;
for(int i = 1; i < nums.length; i++){
cur = nums[i];
if(cur != pre){
// 更新慢指针的值为当前值
nums[low++] = cur;
// 更新pre为当前值
pre = cur;
}
}
return low;
}4-80. 删除有序数组中的重复项II【中等】
给你一个有序数组 nums ,请你**原地** 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 **原地 修改输入数组 **并在使用 O(1) 额外空间的条件下完成。
解法思路及注意点
任然是双指针,但是在26的基础上增加了重复次数的限制
最终代码
public int removeDuplicates(int[] nums) {
if(nums.length == 1){
return 1;
}
int pre = nums[0];
int curRepeatTime = 0;
int cur;
int low = 1;
for(int i = 1; i < nums.length; i++){
cur = nums[i];
if(cur != pre){
// 更新慢指针的值为当前值
nums[low++] = cur;
// 更新pre为当前值
pre = cur;
// 重置重复次数
curRepeatTime = 0;
} else{
// 当前值和前一个值相等
curRepeatTime++;
if (curRepeatTime < 2){
// 重复次数没超过两次
nums[low++] = cur;
}
}
}
return low;
}5-169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。
解法思路及注意点
- 没有说是有序的就可以用排序的思路去做,但是比较赖皮
- 老老实实用map去记录每个数字出现的最大次数,但是不要记录完之后再遍历一次map得到最大的结果,而是再记录过程中维护当前出现最多次数的值,遍历结束直接返回即可
最终代码
/**
* map写法
*/
public int majorityElement(int[] nums) {
int curMaxTime = 0;
int curMaxNum = nums[0];
Map<Integer, Integer> timeOfNum = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int time = timeOfNum.getOrDefault(nums[i], 0);
timeOfNum.put(nums[i], time + 1);
if (curMaxTime < time + 1) {
curMaxNum = nums[i];
curMaxTime = time + 1;
}
}
return curMaxNum;
}
/**
* 赖皮写法
*/
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length / 2];
}6-189. 轮转数组【中等】
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]解法思路及注意点
这道题目纯纯是一道数学题,有些逻辑一下看出来的话就很简单
- 首先是k需要取模,得到最终需要轮转的位数
- 其次,轮转数组,需要三次反转,第一次将整个数组反转,接下来两次即将前一半和后一半反转
最终代码
public void rotate(int[] nums, int k) {
int length = nums.length;
k %= length;
if(k == 0){
return;
}
// 先全部反转
reverse(nums, 0, length -1);
// 再各自反转
reverse(nums, 0, k - 1);
reverse(nums, k, length -1);
}
// 反转数组
public void reverse(int[] nums, int left, int right) {
while(left < right) {
int temp = nums[left];
nums[left++] = nums[right];
nums[right--] = temp;
}
}7-121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5解法思路及注意点
这道题目有要求必须买入在卖出之前,其次,买卖不能在同一天;只能买卖一次
- 买入价【尽可能低】(注意不一定是最低),满足这个要求利润才可能高
- 其二是利润最高,这个目的是最终目的
- 随着买入价的遍历更新维护【当前最大利润】的更新,最终结果就是最大的利润
所以这道题目最后的minBuy并不一定是最后得到最高利润时的买入价,他是动态变化的,一直从开始遍历到末尾
最终代码
public int maxProfit(int[] prices) {
// 根据题意,有两个目的,其一是买入价【尽可能低】(注意不一定是最低),满足这个要求利润才能高
// 其二是利润最高,这个目的是最终目的
// 随着买入价的遍历更新维护【当前最大利润】的更新,最终结果就是最大的利润
int maxProfit = 0;
int minBuy = Integer.MAX_VALUE;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < minBuy) {
// 切换当前的最低买入价
minBuy = prices[i];
}else {
maxProfit = prices[i] - minBuy > maxProfit ? prices[i] - minBuy : maxProfit;
}
}
return maxProfit;
}8-122. 买卖股票的最佳时机II【中等】
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。解法思路及注意点
这道题和121的区别在于,可以多次买入卖出,但是仍然要求任意一天最多能有一张股票,要得到最后最高的利润,其实就是要把期间【所有股票上升期】都赚到,这样就能保证把所有的利润都赚到,得到最高利润。
有一些贪心的思路
最终代码
/**
* 贪心:
* 因为可以一直买卖
* 把所有上升期都赚了,就是最大利润
*/
public int maxProfit(int[] prices) {
int pre = prices[0];
int res = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] - pre > 0) {
res += (prices[i] - pre);
}
pre = prices[i];
}
return res;
}9-55. 跳跃游戏【中等】
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度 。判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。解法思路及注意点
逆向思维,能从最开始跳到最后一步,说明从最后一步可以回到最开始
分析步骤:
- 对于最后一个位置,一定是由前一步跳到,那么压力就来到了倒数第二个位置
- 如果说倒数第二个位置可以跳到最后一个位置,那么只需要保证可以跳到倒数第二个位置就好啦!
- 如果说倒数第二个位置不能跳到最后一个位置,那么压力就来到了倒数第三个位置
- 如果说倒数第三个位置可以跳到最后一个位置,那么他起码要有跳1+1=2个步长的能力
- 如果说倒数第三个位置不能跳到最后一个位置,那么压力就来到了倒数第四个位置
- ...
综上述,就是逻辑前移的步骤,一直前移到第一个位置,满足要求既可以跳过去,否则跳不过去
某一个位置调不到目标位置,那么他的前一个位置就要面临多跳一步的压力
最终代码
public boolean canJump(int[] nums) {
int need = 1;
for(int i = nums.length -2; i >= 0; i--) {
if(nums[i] >= need) {
// 满足最低要求,逻辑前移,need重置为1
need = 1;
continue;
}
// 不满足要求,压力给到前一个位置,需要多跳一步的能力
need++;
}
// 走到这里如果need不是1说明最后一次也不满足要求,跳不过去,否则可以
return need != 1 ? false : true;
}10-45. 跳跃游戏II【中等】
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳1步,然后跳3步到达数组的最后一个位置。解法思路及注意点
这一次和55的区别在于,可以跳到终点,但是重点在于最少跳跃的次数,不在于哪一次跳到了哪一个位置
所以我们可以把每一次跳跃的覆盖值作为参考,维护这个值,记作curCover初始值是0,跳跃次数jumpTime初始值也是0
比如从起点起,第一次跳跃的跳跃覆盖最远处是nums[0],那么第二次跳跃的【起点】就在curCover + 1 ~ nums[0]之间
在这个范围之内获取第二次跳跃所能覆盖的最远处,就是比较:Math.max(curCover, i + nums[i])
i + nums[i]代表的正式当前起点所能覆盖到的最远处,因此取最大值即可,当curCover覆盖到最后一个位置,就可以结束了
最终代码
public int jump(int[] nums) {
// 不关心某一步到底跳到了哪里,而是关心每一步跳完最远能覆盖到哪个下标
// 这样只需要关心哪一次跳跃覆盖到了最后一个下标即可
int curCover = 0; // 表示当前覆盖值的下标在0,对应起始状态
int jumpTime = 0; // 初始第一次是0
int left = 0; // 初始第一次是1
while(curCover < nums.length - 1){
// 表示只要当前没有覆盖到最后一位就还需要遍历
jumpTime++;
int temp = curCover;
for(int i = left; i <= temp; i++){
// 遍历从当前覆盖范围内所有起跳点,得到这次最大的cover=i+nums[i]
curCover = Math.max(curCover, i + nums[i]);
}
left = temp + 1;
}
return jumpTime;
}11-274. H指数【中等】
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 **h 指数 。 根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 **是指他(她)至少发表了 h 篇论文,并且 **至少 **有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值, **h 指数 **是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。解法思路及注意点
关键在于理解H指数的含义,说白了就是求有【x】个数都大于等于【x】;
所以题目的关键在于排序以后的检索
最终代码
public int hIndex(int[] citations) {
// h指数说白了就是数有几个数都大于等于几,所以可以给数组排序,逆序遍历
Arrays.sort(citations);
int i = citations.length - 1;
int hIndex = 0;
// 因为这里hIndex是从0开始算的,必须是大于而不是大于等于,即情况是有1篇等于0的情况,这不符合
while(i >= 0 && citations[i] > hIndex) {
hIndex++;
i--;
}
return hIndex;
}12-380. O(1)时间插入、删除和获取随机元素【中等】
实现RandomizedSet 类:
RandomizedSet()初始化RandomizedSet对象bool insert(int val)当元素val不存在时,向集合中插入该项,并返回true;否则,返回false。bool remove(int val)当元素val存在时,从集合中移除该项,并返回true;否则,返回false。int getRandom()随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 **相同的概率 ** 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
示例:
输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]解法思路及注意点
体现功力的时候,这道题目上来就会让人觉得直接一个set不就秒了吗?
但是到最后一个随机访问,需要一个Random获取一个下标,而Set是随机顺序的,不提供根据索引获取的api,所以就必须要有一个类似下标索引的结构
那么现在有两个可供选择:list和map
而答案是list和map一起使用,这是为啥???主要是考虑到要保证O(1)复杂度随机访问
上面提到,Set并不支持下标获取元素,这样实现getRandom 就必须每次将Set重构成一个List,然后随机访问,然而将Set重构成List时间复杂度为O(n),这一点不符合要求!!!
所以我们需要List结构维护元素的顺序,主要是提供下标随机访问的能力,那么Set就完全可以升级成Map配合List存储数据的下标,这样一来就可以保证操作的O( 1)复杂度。
所以为什么下面代码中要对list和map一起操作,主要就是考虑到要用List提供下标随机访问的能力
最终代码
class RandomizedSet {
List<Integer> nums;
Map<Integer, Integer> indices;
Random random;
public RandomizedSet() {
nums = new ArrayList<Integer>();
indices = new HashMap<Integer, Integer>();
random = new Random();
}
public boolean insert(int val) {
if (indices.containsKey(val)) {
return false;
}
int index = nums.size();
nums.add(val);
indices.put(val, index);
return true;
}
public boolean remove(int val) {
if (!indices.containsKey(val)) {
return false;
}
int index = indices.get(val);
int last = nums.get(nums.size() - 1);
nums.set(index, last);
indices.put(last, index);
nums.remove(nums.size() - 1);
indices.remove(val);
return true;
}
public int getRandom() {
int randomIndex = random.nextInt(nums.size());
return nums.get(randomIndex);
}
}13-283. 除自身以外数组的乘积【中等】
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 **不要使用除法,**且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]解法思路及注意点
题目的重点在于理解“前缀积“和”后缀积”的意义,为了代码编写方便,其实也就是省去一下无意义的边界讨论,需要对前缀和后缀的意义做界定
- 前缀积:除了本身以外之前的元素乘积
- 后缀积:除了本身以外之后的元素乘积
所以最后要求的结果数组,answer[i] = pre[i] * suf[i],这样就可以省去无意义的边界条件,用统一的计算思路
最终代码
public int[] productExceptSelf(int[] nums) {
// 维护前缀乘积和后缀乘积
int[] prefixArray = new int[nums.length];
int[] suffixArray = new int[nums.length];
prefixArray[0] = 1;
suffixArray[nums.length - 1] = 1;
int[] answer = new int[nums.length];
int i = 1, j = nums.length - 2;
for(;i < nums.length && j >= 0; i++, j--){
prefixArray[i] = nums[i - 1] * prefixArray[i - 1];
suffixArray[j] = nums[j + 1] * suffixArray[j + 1];
}
// 前缀乘积和后缀乘积已经算完,直接录入结果
for(int k = 0; k < nums.length; k++) {
answer[k] = prefixArray[k] * suffixArray[k];
}
return answer;
}14-134. 加油站【中等】
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 * 保证* 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。解法思路及注意点
看到的 精辟 的解释:亏空最严重的一个点必须放在最后一步走,等着前面剩余的救助
所以核心就是找到,在哪一个节点时 净消耗量 达到最大,这一点只能在最后一个节点出现,题目的要求是环路的,所以该节点的下一个节点就是出发点
找净消耗量 达到最大即找到 净消耗量极小值点 ,这一点可以维护净消耗量,遍历动态更新,同时题目的要求是走完全程,这就代表不管选择哪一个点作为出发点,全局消耗的油量以及添加的油量都是固定的,这样一来遍历到最后的净消耗量也就能反应到底能不能走完全程了。这时不存在解,否则可以。
最终代码
public int canCompleteCircuit(int[] gas, int[] cost) {
int len = gas.length;
int spare = 0; // 代表净消耗量
int lowSpare = Integer.MAX_VALUE; // 净消耗量极小值点
int lowSpareIndex = 0;
for (int i = 0; i < len; i++) {
spare += gas[i] - cost[i];
if (spare < lowSpare) {
lowSpare = spare;
lowSpareIndex = i;
}
}
return spare < 0 ? -1 : (lowSpareIndex + 1) % len;
}15-135. 分发糖果【困难】
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。 你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。解法思路及注意点
学习,一个赋初值的小技巧
int[] num = IntStream.generate(() -> 10).limit(5).toArray();学习经验:有些事情需要正着来一遍再逆着来一遍,就可以耦合
我们需要确认条件,👈👉左右两边的条件
从左到右遍历(正方向):左边的能力高的要比右边能力低的多获取一个
从右到左遍历(逆方向):右边的能力高的要比左边能力低的多获取一个
这样连续两次for的遍历之后,双方的条件就都满足了
最终代码
虽然不是最佳的,但是看得比较清楚明白
/**
* 左右各遍历一次
*
* @param ratings
* @return
*/
public int candy(int[] ratings) {
int length = ratings.length;
if (length == 1) {
return 1;
}
// 表示每个孩子相对获取糖果的数量
int[] num = new int[length];
int total = length; // 每个小孩子初始化一个糖果,后续根据遍历条件增加即可
for (int i = 0; i < length - 1; i++) {
// 主要条件是要看ratings的能力, 能力高的要比能力低的多获取一个
int inc = Math.abs(num[i + 1] - num[i]) + 1;
if (ratings[i] > ratings[i + 1] && num[i] <= num[i + 1]) {
num[i] += inc;
total += inc;
} else if (ratings[i] < ratings[i + 1] && num[i] >= num[i + 1]) {
num[i + 1] += inc;
total += inc;
}
}
// 二次确认,这是需要反过来确认,就是把上面代码逆序的情况写出来
for (int i = length - 1; i > 0; i--) {
int inc = Math.abs(num[i] - num[i - 1]) + 1;
if (ratings[i] > ratings[i - 1] && num[i] <= num[i - 1]) {
num[i] += inc;
total += inc;
} else if (ratings[i] < ratings[i - 1] && num[i] >= num[i - 1]) {
num[i - 1] += inc;
total += inc;
}
}
return total;
}16-42. 接雨水【困难】
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。解法思路及注意点
求每一列上面积攒多少水,动态规划,每一列对应两个指标,左边最高的高度以及右边最高的高度
然后根据左右两端最高高度的最小值,去和当前列比较,就能知道当前列上面有没有水
如果那个最小值比当前列还小,说明当前列不可能积水;否则会积水,而且积水量是最小值-当前列高度
整体上看起来有点和“283. 除自身以外数组的乘积”有点类似,都有前缀后缀的意义,但这道题更加隐晦需要有推理出来的能力
最终代码
public int trap(int[] height) {
// 求每一列上面积攒多少水,动态规划,每一列对应两个指标,左边最高的高度以及右边最高的高度
// 然后根据左右两端最高高度的最小值,去和当前列比较,就能知道当前列上面有没有水
// 如果那个最小值比当前列还小,说明当前列不可能积水;否则会积水,而且积水量是最小值-当前列高度
int sum = 0;
int[] max_left = new int[height.length];
int[] max_right = new int[height.length];
for (int i = 1; i < height.length - 1; i++) {
max_left[i] = Math.max(max_left[i - 1], height[i - 1]);
}
for (int i = height.length - 2; i >= 0; i--) {
max_right[i] = Math.max(max_right[i + 1], height[i + 1]);
}
for (int i = 1; i < height.length - 1; i++) {
int min = Math.min(max_left[i], max_right[i]);
if (min > height[i]) {
sum += min - height[i];
}
}
return sum;
}17-13. 罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。 通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入:s = "III"
输出: 3解法思路及注意点
首先是要对单个【罗马数字】和【整数】之间的转换提供方法
接下来是理解规则:罗马数字的简单概括就是把字符串上的每一位代表的整数都加起来,但是这之间又有一个特殊的规则必须要遵守:
- 小的数字如果在大的数字之前,这一位小的数字需要作为减数减去
所以最后不管正序还是逆序去实现都可以
最终代码
public int romanToInt(String s) {
int sum = 0;
int preNum = getValue(s.charAt(0));
for(int i = 1; i < s.length(); i++){
int num = getValue(s.charAt(i));
if(preNum < num){
// 说明前面的这个数比这一位数小,是减法的情况
sum -= preNum;
}else {
sum += preNum;
}
preNum = num;
}
// 此时preNum 指向最后一个值
return sum + preNum;
}
private int getValue(char ch) {
switch(ch) {
case 'I': return 1;
case 'V': return 5;
case 'X': return 10;
case 'L': return 50;
case 'C': return 100;
case 'D': return 500;
case 'M': return 1000;
default: return 0;
}
}18-12. 整数转罗马数字【中等】
七个不同的符号代表罗马数字,其值如下:
| 符号 | 值 |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则:
- 如果该值不是以 4 或 9 开头,请选择可以从输入中减去的最大值的符号,将该符号附加到结果,减去其值,然后将其余部分转换为罗马数字。
- 如果该值以 4 或 9 开头,使用 减法形式,表示从以下符号中减去一个符号,例如 4 是 5 (
V) 减 1 (I):IV,9 是 10 (X) 减 1 (I):IX。仅使用以下减法形式:4 (IV),9 (IX),40 (XL),90 (XC),400 (CD) 和 900 (CM)。 - 只有 10 的次方(
I,X,C,M)最多可以连续附加 3 次以代表 10 的倍数。你不能多次附加 5 (V),50 (L) 或 500 (D) 。如果需要将符号附加4次,请使用 减法形式。
给定一个整数,将其转换为罗马数字。
示例 1: **输入:**num = 3749 输出: "MMMDCCXLIX" 解释:
3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
700 = DCC 由于 500 (D) + 100 (C) + 100 (C)
40 = XL 由于 50 (L) 减 10 (X)
9 = IX 由于 10 (X) 减 1 (I)
注意:49 不是 50 (L) 减 1 (I) 因为转换是基于小数位
提示:
1 <= num <= 3999解法思路及注意点
根据提示就是这道题只涉及给出的几个符号之间的转换,不涉及其他字母
.............暴力模拟,除法的本质是减法😄
最终代码
// 暴力模拟
int[] values = { 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1 };
String[] symbols = { "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I" };
// 整个题目的最大值是3999,也就是最大是四位数,只涉及题目中给出的罗马字母
public String intToRoman(int num) {
StringBuilder result = new StringBuilder();
for(int i = 0; i < values.length; i++){
int value = values[i];
String symbol = symbols[i];
// 除法的本质是减法 = =乐
while (num >= value) {
num -= value;
result.append(symbol);
}
if (num == 0) {
break;
}
}
return result.toString();
}19-58. 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = "Hello World"
输出:5
解释:最后一个单词是“World”,长度为 5。提示:
1 <= s.length <= 104s仅有英文字母和空格' '组成s中至少存在一个单词
解法思路及注意点
- 解法一:API战士!!!🤣
- 解法二:暴力!直接逆序找到最后一个单词的开头的索引,然后return字数
踩坑点,这道题并不是说标准的英文规范,空格是出现是随机的,并且也不一定出现时只有一个空格,就算是最后一个单词,他的后面也可能还有空格
最终代码
public int lengthOfLastWord(String s) {
String[] split = s.split(" ");
return split[split.length - 1].length();
}
public int lengthOfLastWord(String s) {
int index = s.length() - 1;
while (s.charAt(index) == ' ') {
index--;
}
int wordLength = 0;
while (index >= 0 && s.charAt(index) != ' ') {
wordLength++;
index--;
}
return wordLength;
}20-14. 最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。解法思路及注意点
【二分查找】
显然,最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。用 minLength 表示字符串数组中的最短字符串的长度,则可以在 [0,minLength] 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 mid,判断每个字符串的长度为 mid 的前缀是否相同,如果相同则最长公共前缀的长度一定大于或等于 mid,如果不相同则最长公共前缀的长度一定小于 mid,通过上述方式将查找范围缩小一半,直到得到最长公共前缀的长度。
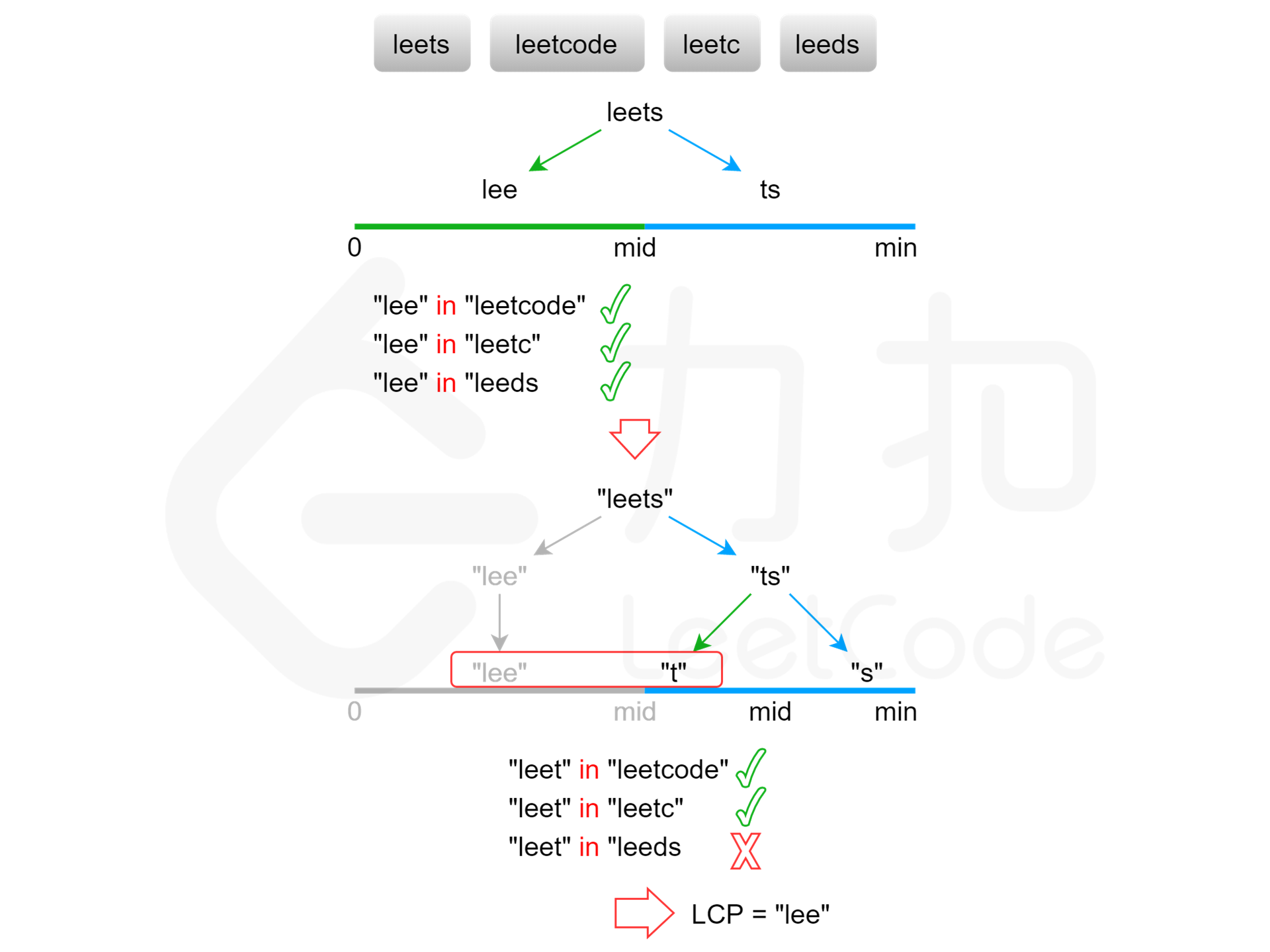
作者:力扣官方题解
力扣给了四种解法,虽然这道题是简单题,但是【最长公共前缀】是一个很经典的算法问题,有比如递归分治、暴力破解的方法,这个二分的逻辑非常妙🤣
最终代码
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
int minLength = Integer.MAX_VALUE;
for (String str : strs) {
minLength = Math.min(minLength, str.length());
}
// 先找到最短的字符串,最长公共前缀的长度肯定低于这个字符串长度
int low = 0, high = minLength;
// 用二分的逻辑,找到到底公共前缀的长度在minLength的哪个区间
while (low < high) {
int mid = (high - low + 1) / 2 + low;
// 尝试mid是否满足最长公共子前缀,满足就再尝试多一点,不满足说明就低于mid
if (isCommonPrefix(strs, mid)) {
low = mid;
} else {
high = mid - 1;
}
}
return strs[0].substring(0, low);
}
// 决策length是否是strs的公共前缀
public boolean isCommonPrefix(String[] strs, int length) {
String str0 = strs[0].substring(0, length);
int count = strs.length;
for (int i = 1; i < count; i++) {
String str = strs[i];
for (int j = 0; j < length; j++) {
if (str0.charAt(j) != str.charAt(j)) {
return false;
}
}
}
return true;
}21-151. 反转字符串中的单词【中等】
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用 至少一个空格将字符串 中的 单词 分隔开。
要求:返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
**注意:**输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格。示例 3:
输入:s = "a good example"
输出:"example good a"
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。解法思路及注意点
这道题同样还是一眼可以API解决的,但是算法中往往用API秒解的是不希望你用的方法,只能“等通知”吧😭
其实这道题和“58.最后一个单词的长度”很像,前者是逆序查找最后一个单词,那我们可以顺着其思路,一直往前查找直到整个字符串被我们找完,其实找到单词的逻辑是很简单的,无非是从第一个非空格位置开始,找到下一个空格位这样是一个完整的单词, 但难在空格拼接逻辑,怎样控制最后一个单词的最后不追加空格呢?
这个问题详细看第四个方法,也是强推的处理,相信看完就会明白!👌
::: success 标题
这个api总是被忽略,用于将字符数组的一部分转换为字符串。它的作用是**从字符数组的指定位置开始,提取指定长度的字符,并将其转换为一个新的字符串 **。
String str = String.valueOf(char, offset, count);:::
最终代码
- 低效api
- 时间复杂度:O(n),其中 n 为输入字符串的长度。
- 空间复杂度:O(n),用来存储字符串分割之后的结果。
public String reverseWords(String s) {
String str = s.trim();
String[] splits = str.split(" ");
List<String> collect = Arrays.stream(splits)
.filter(split -> !split.isEmpty())
.collect(Collectors.toList());
StringBuffer result = new StringBuffer();
for (int i = collect.size() - 1; i >= 0; i--) {
result.append(collect.get(i));
if (i > 0) {
result.append(" ");
}
}
return result.toString();
}- 高效api
- 时间复杂度:O(n),其中 n 为输入字符串的长度。
- 空间复杂度:O(n),用来存储字符串分割之后的结果。
public String reverseWords(String s) {
// 除去开头和末尾的空白字符
s = s.trim();
// 正则匹配连续的空白字符作为分隔符分割
List<String> wordList = Arrays.asList(s.split("\\s+"));
Collections.reverse(wordList);
return String.join(" ", wordList);
}- 借鉴“58.最后一个单词的长度” ,逆序查找,找到每一个单词然后追加,但是这个方法并没能很好的控制空格的追加逻辑,在4中做了优化
public String reverseWords(String s) {
int index = s.length() - 1;
StringBuffer result = new StringBuffer();
while (index >= 0) {
// 向前寻找字符串的末尾
while (index >= 0 && s.charAt(index) == ' ') {
index--;
}
// 看index是否已经到了最开始
if (index < 0) {
break;
}
int wordLastIdx = index;
while (index >= 0 && s.charAt(index) != ' ') {
index--;
}
// 找到一个完整单词,此时加入result,substring是左闭右开区间,且此时index是空格
result.append(s.substring(index + 1, wordLastIdx + 1) + " ");
}
String string = result.toString();
return string.trim();
}- 对3的方法做了优化,空格追加的逻辑更加清晰【强推】
public String reverseWords(String s) {
s = s.trim();
if (s.length() == 1 && !s.equals(" ")) {
return s;
}
// 已经去除了前面和后面的空格的字符串,将其处理,取出每一个字符串
char[] sToChar = s.toCharArray();
StringBuffer newStr = new StringBuffer();
int count = 0;
// 由trim知道第一个字符是非" "字符,下面的循环给sb追加单词的逻辑是从一个单词的结尾开始找到这个单词前的一个空格时触发
// 所以最后一个要找的单词(也就是trim后的字符串的第一个单词),添加的逻辑并不在这个循环中,这也是为了单词之间" "的考虑,追加最后一个单词时不需要加空格
for (int i = sToChar.length - 1; i >= 0; i--) {
// 找到一个完整的单词,需要添加了
if (sToChar[i] == ' ') {
newStr.append(String.valueOf(sToChar, i + 1, count));
newStr.append(" ");
// 找到一次重置
count = 0;
// 找到' '要确保其前面不是空格
while (sToChar[i - 1] == ' ') {
i--;
}
} else {
count++;
}
}
// 停在最开始的位置,这是第一个单词,也要输出
newStr.append(String.valueOf(sToChar, 0, count));
return new String(newStr);
}22-6. Z字形转换【中等】
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。 请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I解法思路及注意点
分析过程 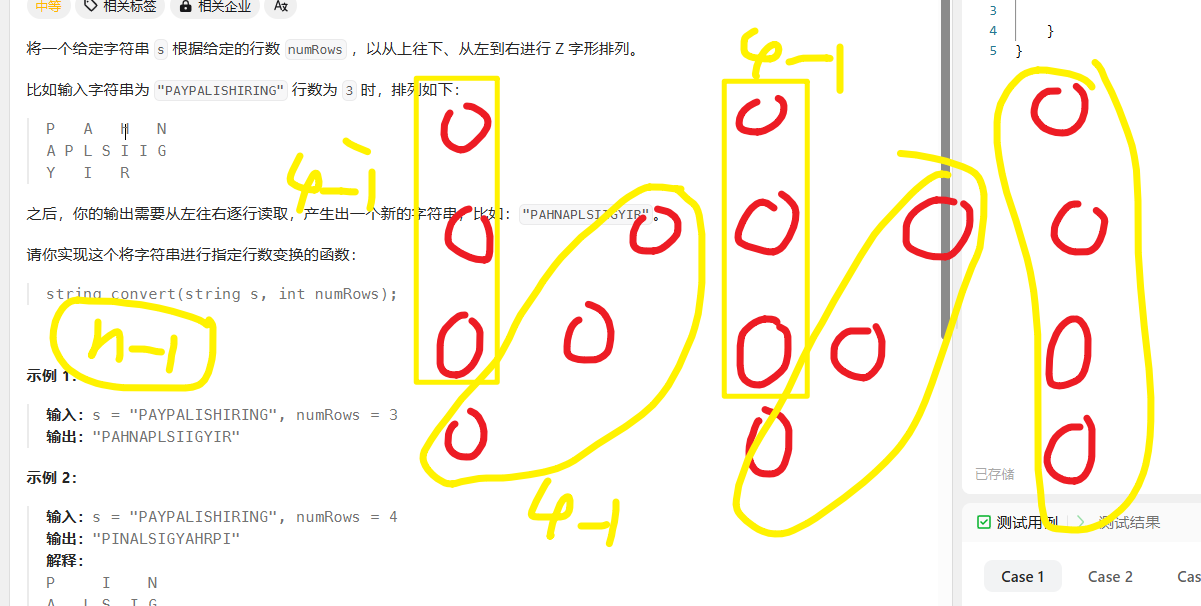
上图可能有点抽象,但是大致抽象出了步骤,每个操作单元数是 unit = numRows - 1 ,从上到下纵向一组,然后从左到右斜向一组,我们只需要对给定的数组的长度对unit取模,就知道要进行几次单元操作,又通过这个结果和2的整数关系,我们就知道最后一次操作单元是纵向还是斜向!!!
🌟太聪明了
接下来是最关键的思路,看到这种题目第一反应可能是构造一个二维数组,然后给数组的每一个位置填充元素,最后遍历这个二维数组即可,但是有点浪费内存空间,下标的逻辑关系一时半会儿想不出来,及时想出来也很可能出错,于是我抽象出了更精简的实现!StringBuilder!
没错,就是把每一行都抽象成StringBuffer,这样就相当于每次操作就是给对应的StringBuilder追加操作,最后也可以省略掉二维数组那样下标的逻辑,只要把个 numRows个StringBuilder一起合并就好啦!
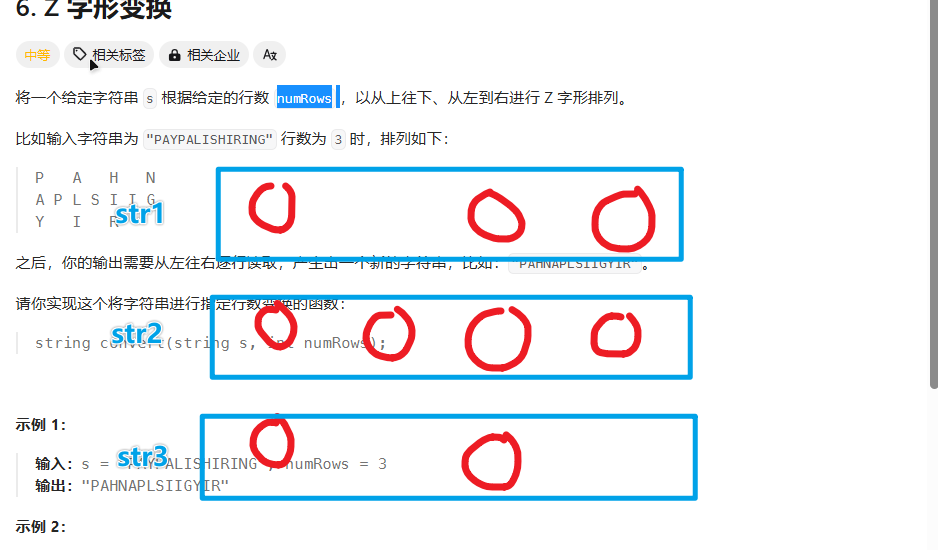
【核心点】:为了省去很多复杂的逻辑判断,我们可以给纵向和斜向定义一个flag,可以发现每当执行到numRows-1或者0 的时候,就是开始改变方向的shi
最终代码
public String convert(String s, int numRows) {
if(numRows < 2) return s;
List<StringBuilder> rows = new ArrayList<StringBuilder>();
for(int i = 0; i < numRows; i++) rows.add(new StringBuilder());
int i = 0, flag = -1;
for(char c : s.toCharArray()) {
rows.get(i).append(c);
if(i == 0 || i == numRows -1) flag = - flag;
i += flag;
}
StringBuilder res = new StringBuilder();
for(StringBuilder row : rows) res.append(row);
return res.toString();
}23-125. 验证回文串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 **回文串 ** 。 字母和数字都属于字母数字字符。 给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。示例 2:
输入:s = "race a car"
输出:false
解释:"raceacar" 不是回文串。示例 3:
输入:s = " "
输出:true
解释:在移除非字母数字字符之后,s 是一个空字符串 "" 。
由于空字符串正着反着读都一样,所以是回文串。解法思路及注意点
这题比较简单,按照要求将原字符串中的无效字符剔除即可,最终得到目标字符串,双指针两头一起比较,一旦有不一样的说明就不会是回文结构
踩坑点:sb.append((char)(s.charAt(i) + 32));
这里非常容易忘记类型转换,否则这里因为char和int类型计算会自动升级为int类型,这里追加字符就直接变成int整形的数字而不是想要的字符了。很关键!
最终代码
public boolean isPalindrome(String s) {
StringBuffer sb = new StringBuffer();
for (int i = 0; i < s.length(); i++) {
if ((s.charAt(i) >= '0' && s.charAt(i) <= '9') ||
(s.charAt(i) >= 'a' && s.charAt(i) <= 'z')) {
// 是数字或小写字母
sb.append(s.charAt(i));
} else if (s.charAt(i) >= 'A' && s.charAt(i) <= 'Z') {
// 是大写字母,大写转小写,加32
sb.append((char)(s.charAt(i) + 32));
}
}
String targetStr = sb.toString();
for(int i = 0, j = targetStr.length() - 1; i < j; i++, j--){
if(targetStr.charAt(i) != targetStr.charAt(j)){
return false;
}
}
return true;
}24-392. 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde" 的一个子序列,而"aec"不是)。
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false解法思路及注意点
题目要保证s串所有字符要出现在t串中,且保持相对顺序,只需要定义双指针,tIndex遍历t串,sIndex遍历s串,当且仅当sIndex指向的字符和tIndex指向的字符相同时,sIndex才扫描下一个,其他情况下tIndex都自增。
这样就保证了sIndex在搜索的过程中维持t串的相对顺序,最后如果sIndex成功遍历完毕,那么s串就是t串的子序列,否则不是
最终代码
// 双指针
public boolean isSubsequence(String s, String t) {
int sLen = s.length();
int tLen = t.length();
if (sLen == 0) {
return true;
}
int sIndex = 0, tIndex = 0;
while (sIndex < sLen && tIndex < tLen) {
if (s.charAt(sIndex) == t.charAt(tIndex)) {
// 找到s和t相等的值
sIndex++;
}
tIndex++;
if(sIndex == sLen){
// 说明s的所有字符切顺序保持相对位置
return true;
}
}
return false;
}25-167. 两数之和II-输入有序数组【中等】
给你一个下标从 1 开始的整数数组 numbers ,该数组已按** 非递减顺序排列 **,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。 以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。 你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。 你所设计的解决方案必须只使用常量级的额外空间。 示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。解法思路及注意点
题目给出两点关键要求:结果只有一个有效解,给的数组是非递减排列的 (但是注意并没有说无解的情况,所以其实这道题还有一点是隐含的如果无解时怎么办)
为什么这道题是典型的双指针?
数组的非递减性排列给这道题非常大的关键。从左边和右边一起,以右边为快指针,如果当前左边+右边比target大,只能说明是右边的数更大引起的,只能让右边的数往前走;反之则应该让左边的数右移动。
最终代码
public int[] twoSum(int[] numbers, int target) {
int i = 0;
int j = numbers.length - 1;
while (i < j) {
int sum = numbers[i] + numbers[j];
if (sum < target) {
i++;
} else if (sum > target) {
j--;
} else {
return new int[] { i + 1, j + 1 };
}
}
return new int[] { -1, -1 };
}26-11. 盛最多水的容器【中等】
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 **说明:**你不能倾斜容器。
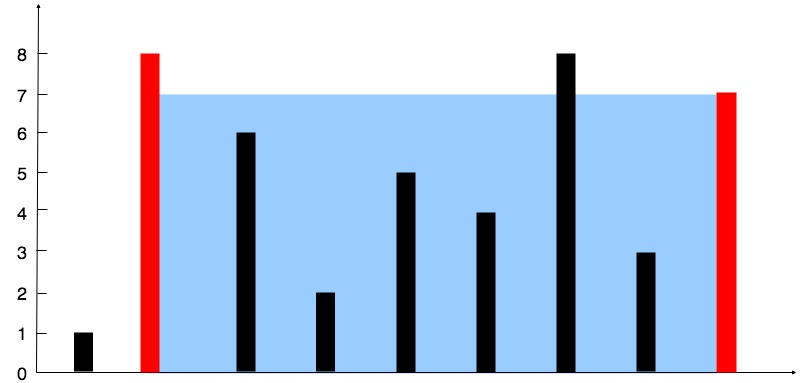
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1]
输出:1解法思路及注意点
和167.两数只和II类似,双指针从两侧逐步向内移动,题目要求的是获得最大的面积,只有移动较小的一方才可能获得到更高的值,以此获取加大面积的可能,最后结束在两个指针相遇的时候,同时维护期间的最大面积,最后返回即可
最终代码
public int maxArea(int[] height) {
int length = height.length;
int maxArea = 0;
for (int left = 0, right = length - 1; left < right;) {
int leftHeight = height[left];
int rightHeight = height[right];
maxArea = Math.max(maxArea, (right - left) * Math.min(leftHeight, rightHeight));
// 因为下一次将要缩窄范围,但是可以在这里限制条件,减少无效循环
// 如果要缩窄的一边缩窄后更矮了,那只可能更小,继续向前即可
if (leftHeight <= rightHeight) {
// 左边更小
while (left < right && height[left] <= leftHeight)
left++;
} else {
while (left < right && height[right] <= rightHeight)
right--;
}
}
return maxArea;
}27-15. 三数之和【中等】
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。 **注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。2 4 8 k = 3
解法思路及注意点
这道题和167.两数之和是一样的题目,但其实难在如何去除重复的解
首先,三数之和为0,我们可以设计快指针是最左侧,这样三数之和的要求就可以转换为两数之和的要求
其次,我们对数组排序,那么刚刚转换的两数之和就彻底和167题一样了,我们可以再对其做一个双指针的筛选
最后也是难点,即题目要求我们返回的是“三数之和为零”的三元组,在一个三元组中要求这三个数是不同位置上的数字,且三元组的三个数的顺序没有区分性,这就要求我们去想什么时候会有重复项,或者说,我们如何避免一些重复的计算工作?
拿最左侧快指针为例,每一次循环的时候我们都以它
最终代码
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> listNest = new ArrayList<>();
if (nums.length < 3) {
// 直接返回空
return listNest;
}
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2; i++) {
Integer num1 = nums[i];
if (num1 > 0) {
// 因为是有序的,当nums[1]为正数时,其他两个数不可能相加是负数
break;
}
if (i > 0 && nums[i] == nums[i - 1]) {
// 避免重复
continue;
}
Integer target = -num1;
// 两个指针分别知道i的后一位和列表的最后一位
int front = i + 1;
int end = nums.length - 1;
while (front < end) {
int sumOfTwo = nums[front] + nums[end];
if (sumOfTwo == target) {
listNest.add(Arrays.asList(nums[i], nums[front], nums[end]));
front++;
end--;
// 这里需要做一个防重复的处理
while (front < end && nums[front] == nums[front - 1]) {
// 相同的数值,第一个指针从左到右前进一步
front++;
}
while (front < end && nums[end] == nums[end + 1]) {
// 相同的数值,第一个指针从右到左前进一步
end--;
}
} else if (sumOfTwo > target) {
end--;
} else {
front++;
}
}
}
return listNest;
}28-1143. 最长公共子序列【中等】
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。解法思路及注意点


最终代码
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}29-49. 字母异位词分词【中等】
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]示例 2:
输入: strs = [""]
输出: [[""]]示例 3:
输入: strs = ["a"]
输出: [["a"]]解法思路及注意点
字母异位词,关键是要总结出一点:所谓异位词构成的所有词,特点就是构成他们的字符是完全一样的,即每个字符出现的次数是相等的
所以可以有两种思路:
- 直接给该字符串的字符数组排序(Arrays.sort(char[] str)),则由这个异位词分词构成的字符串都符合
- 搞一个Word类,这个类维护一个int[26]数组,代表构成某个word的二十六个字符出现的次数,只要完全一样,那他们就是异位词
最终代码
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<>();
for (String str : strs) {
char[] array = str.toCharArray();
Arrays.sort(array);
String key = new String(array);
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
// 添加完以后修改
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}30-128. 最长连续序列【中等】
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9示例 3:
输入:nums = [1,0,1,2]
输出:3解法思路及注意点
这道题,主要是理清楚,连续序列有什么特点,我们可以抽象出一个连续序列的共同特点如下:
- 要想成为这个序列的开头head,那么head - 1就不在给出的数组中
- 要想成为这个序列的结尾end,那么end + 1就不在给出的数组中
- 同理,如果是序列的中间元素,那么前驱和后继都在
题目要求o(n),可以先把所有元素的记录在set中,然后for判断,动态维护一个最长的序列长度,最后返回即可
最终代码
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int num : nums) {
set.add(num);
}
int res = 0;
int count = 0;
// 最长连续序列,如果是开头,就说明比她小1的数不存在
for (int num : set) {
if (!set.contains(num - 1)) {
int curr = num;
count = 1;
// 说明这个数是开头
while (set.contains(curr + 1)) {
count++;
curr++;
}
// 找到了序列的尾部才停下while
res = Math.max(res, count);
}
}
return res;
}31-移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]示例 2:
输入: nums = [0]
输出: [0]解法思路及注意点
双指针经典入门题,快指针遍历,慢指针找到非零数,最后让慢指针走到结尾把赋值最后的数为0即可
最终代码
public void moveZeroes(int[] nums) {
int fast = 0, slow = 0;
int len = nums.length;
for(; fast < len; fast++){
if(nums[fast] != 0){
nums[slow++] = nums[fast];
}
}
for(int i = slow; i < len; i++){
nums[i] = 0;
}
}32-3. 无重复字符的最长子串【中等】
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。解法思路及注意点
本题关键在于【子串】,“子串”和“子序列”是两个不同的概念,前者强调其连续性,而后者强调位置的相对性
这道题可以用【滑动窗口】的做法,即通过移动窗口的过程,动态的维护满足题意的【窗口】的最大长度,最后返回即是答案
我们知道移动的过程是右边界是探索边界,即窗口的滑动是右边驱动的,那么左边界什么时候变动呢?
答案就是当右边界的字符已经存在在该窗口内时,需要左边界向前滑动,直到窗口内不存在右边界的字符,此时才可以把右边界的字符添加进来
所以关键在于 “如何判断右边界的字符已经存在在该窗口内”, 那一定是Set了,所以代码如下
最终代码
public int lengthOfLongestSubstring(String s) {
Set<Character> window = new HashSet<>();
int curLeft = 0;
int maxLen = 0;
for(int right = 0; right < s.length(); right++) {
while(window.contains(s.charAt(right))){
// 一旦当时窗口内存在当前值,因为是子串,及必须保证连续性,必须一直删除直到这个值不在window中
window.remove(s.charAt(curLeft++));
}
// 可以把当前字符添加到窗口中
window.add(s.charAt(right));
maxLen = Math.max(maxLen, right - curLeft + 1); // 更新最大长度
}
return maxLen;
}33-438. 找到字符串中所有的字母异位词【中等】
给定两个字符串 s 和 p,找到 s中所有 p的 **异位词 **的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。** 示例 2:**
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。解法思路及注意点
关于【异位词】的定义,上面有题目已经说过了,这里不再赘述,下面的int[26]就很好理解了,就是二十六个字符的出现次数
这一题也是【滑动窗口】的经典题目,但是下方代码中:不同于一般的【滑动窗口】有明显的窗口滑动的迹象,即不是明确的移动左右边界,而是通过 对左边界字符的出现次数-1 或者 对右边界字符的出现次数+1 变相的实现了窗口的滑动,我们的目的就是要保存某个时刻的窗口( 该窗口满足其中的字符出现次数满足于异位词的出现次数)的左边界,即起始索引
对于异位词的做法,不再赘述,下面的count方法就很好解释
int[] curr = count(s, 0, tLen - 1);关于这行初始化窗口的逻辑,就是对s串从0到tLen-1先获取其字符出现的次数,作为窗口的起始状态,在后续窗口移动过程中,就是对左边界或者右边界的字符进行次数的加减操作,最后于target比对
最终代码
public List<Integer> findAnagrams(String s, String t) {
List<Integer> res = new ArrayList<>();
if (s.length() < t.length()) {
return res;
}
int tLen = t.length();
int[] target = count(t, 0, tLen); // 每次找到的串都得符合target
int[] curr = count(s, 0, tLen - 1);
for (int i = tLen - 1; i < s.length(); i++) {
curr[s.charAt(i) - 'a']++; // 加入当前字符
if (Arrays.equals(target, curr)) {
res.add(i - tLen + 1); // 记录起始索引
}
curr[s.charAt(i - tLen + 1) - 'a']--; // 移除最左边的字符
}
return res;
}
public int[] count(String s, int left, int right) {
int[] res = new int[26];
for (int i = left; i < right; i++) {
res[s.charAt(i) - 'a']++;
}
return res;
}34-560. 和为k的子数组【中等】
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k的子数组的个数 。 子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2示例 2:
输入:nums = [1,2,3], k = 3
输出:2解法思路及注意点
这道题目的官方解答是【子串】,但其实有点【动态规划】的思想
首先我们要把题目转换,题目要求“和为k的子数组”,关键有两个,一是“子数组”,二是“子数组的和为k”
首先“子数组”不同于“子序列”,已经不用再赘述了,就是要求连续;对于【连续】我们就可以设计结构了,这里采取dp的思想
设dp[i]表示nums数组从0~i的和,那么dp[j]表示nums数组从0~j的和,加入i > j,那么显然有dp[i] - dp[j]就代表了nums数组从j+1~i的和
假设从j+1~i这一段满足差值是k,那么我们要求的一个子数组就是j+1~i了
所以上述思路说半天就是逻辑转换的一个过程,我们要找的“子数组”具有连续性,但是又不好判断哪里是起始位置,哪里是结束位置。* 所以我们就可以固定起点变化终点*(所以可以借鉴dp的做法),对这两段数字做差即可。最后满足要求的数组我们对其计数就行啦
最终代码
public int subarraySum(int[] nums, int k) {
int n = nums.length;
int[] pre = new int[n]; // pre[i]代表从0到i的和
// 目标值为k,如果j < i,且pre[j] = pre[i] - k, 那么从j+1到i的和就是 pre[i] - (pre[i] - k) = k
// 所以求子串和为k,其实就是对于每个i求有多少个前缀和是pre[i]-k,这样他们都满足从其下一个位置起到i的和都是k
// 最后累加就是结果
int count = 0;
pre[0] = nums[0];
// 赋值从0到i的值
for (int i = 1; i < n; i++) {
pre[i] = nums[i] + pre[i - 1];
}
// 寻找pre[i] - k 的个数
final Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int i = 0; i < n; i++) {
count += map.getOrDefault(pre[i] - k, 0);
map.put(pre[i], map.getOrDefault(pre[i], 0) + 1);
}
return count;
}35-239. 滑动窗口的最大值【困难】
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7示例 2:
输入:nums = [1], k = 1
输出:[1]解法思路及注意点
这道题其实是模拟了滑动窗口的过程,但是还是有【子串】的意义,即保持连续性
解决的办法是用了【单调栈】,下面梳理单调栈的作用如下:
单调栈的核心思想
单调栈是一种特殊的栈结构,它的特点是栈中的元素始终保持单调性(单调递增或单调递减)。在这道题中,我们使用单调递减栈,即 栈中的元素从栈底到栈顶是递减的。
单调栈的核心作用是:
- 快速找到当前窗口的最大值:栈底元素就是当前窗口的最大值。
- 维护窗口的有效性:当窗口滑动时,移除不在窗口范围内的元素。
- 在遍历数组时,对于当前元素
nums[i],我们需要确保栈中的元素是单调递减的。 - 如果当前元素
nums[i]大于栈顶元素对应的值nums[stack.peek()],说明栈顶元素不可能是当前窗口或后续窗口的最大值,因此将其弹出。 - 重复这个过程,直到栈为空或当前元素
nums[i]小于等于栈顶元素对应的值。 - 最后将当前元素的索引
i压入栈中。
为什么这样做?
- 单调递减栈保证了栈底元素是当前窗口的最大值。
- 弹出比
nums[i]小的元素,确保栈中只保留可能成为最大值的元素。【核心】 - 维护窗口的有效性
- 当窗口滑动时,窗口的左边界会向右移动。如果栈底元素(即当前最大值)已经不在窗口范围内(即
stack.peekLast() <= i - k),则需要将其从栈中移除。 - 这一步确保了栈中的元素始终在当前窗口范围内。
- 当窗口滑动时,窗口的左边界会向右移动。如果栈底元素(即当前最大值)已经不在窗口范围内(即
最终代码
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if (n == 0) {
return new int[0];
}
int[] res = new int[n - k + 1];
Deque<Integer> stack = new LinkedList<>(); // 单调栈
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
// 单调栈遇到大的数就出栈然后把这个数放进去
stack.pop();
}
stack.push(i);
// 接下来看移动窗口的过程中,最大值在不在窗口的最左侧(这决定是否需要出栈)
if (i >= k) {
if (stack.peekLast() <= (i - k)) {
stack.pollLast();
}
}
if (i >= k - 1) {
res[i - k + 1] = nums[stack.peekLast()];
}
}
return res;
}36-76. 最小覆盖子串【困难】
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。 - 如果
s中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。示例 2:
输入:s = "a", t = "a"
输出:"a"
解释:整个字符串 s 是最小覆盖子串。示例 3:
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。解法思路及注意点
这道题还是【子串】类问题,子串类问题大多数可以用【滑动窗口】,这道题也类似
其实这道题目也和之前的题目有点类似,比如【异位词】,只不过这次需要拥有异位词的情况下还保证是子串,那么这也就是说目标子串 >= 异位词的字符数组(联系我们之前的做法,把构成异位词的字符在数组中体现)
在窗口的移动过程中使得该子串符合目标,然后动态维护满足要求的最小长度,最后返回
最终代码
public String minWindow(String s, String t) {
int[] count = new int[256];
int[] target = count(t);
int l = 0;
int r = -1;
int maxL = 0;
int maxR = Integer.MAX_VALUE;
while (l < s.length()) {
if (has(count, target)) {
if (r - l < maxR - maxL) {
// 如果当前已经可以覆盖,那就说明窗口可以缩小
maxR = r;
maxL = l;
}
count[s.charAt(l++)]--;
} else {
if (r == s.length() - 1) {
// 如果窗口已经移动到边儿了
break;
}
// 说明窗口还不能覆盖,窗口得扩大
count[s.charAt(++r)]++;
}
}
return maxR == Integer.MAX_VALUE ? "" : s.substring(maxL, maxR + 1);
}
// 对于英文字符和标点符号的,可以创建一个int[256],因为ASCII码256个字符
// 将t串中的字符记录
int[] count(String t) {
int[] counts = new int[256];
final char[] chars = t.toCharArray();
for (int c : chars) {
counts[c]++;
}
return counts;
}
// 根据上面的函数设置下面的函数,因为我们要求的是最小覆盖子串,所以结果是比t串的字符大于等于的关系
boolean has(int[] s, int[] t) {
for (int i = 0; i < 256; i++) {
if (s[i] < t[i]) { // 根据上面的注释,如果这个条件满足说明当前串还不能覆盖子串
return false;
}
}
return true;
}37-
解法思路及注意点
最终代码
38-
解法思路及注意点
最终代码
39-
解法思路及注意点
最终代码
40-
解法思路及注意点
最终代码